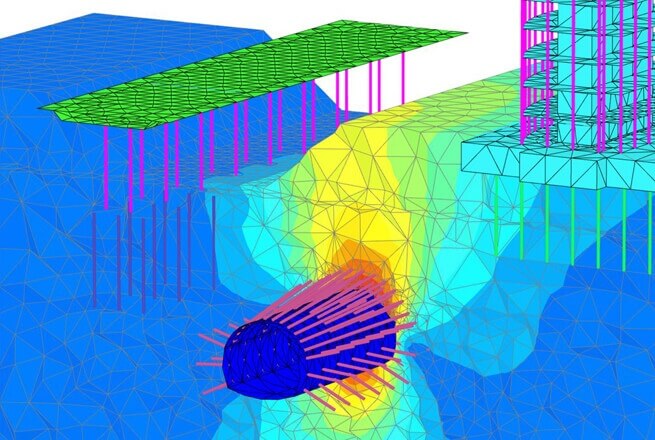
Plaxis programı nedir? Nerelerde kullanılır?
Plaxis sonlu elemanlar programı inşaat mühendisliğinde özellikle geoteknik alanında yararlı bir programdır. Bu program ile özellikle zemin alanında yapılacak uygulamalar Plaxis programı ile modellenerek analiz edilebilmektedir. Örnek vermek gerekirse tünel uygulamaları, yüzeysel ve derin temellerin analizi, kazık ve ankraj uygulamalarında kullanılmaktadır.
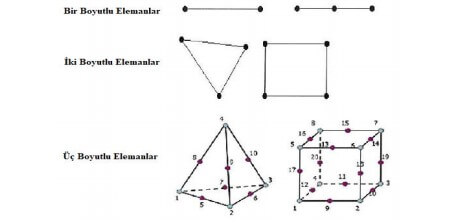
Plaxis, sonlu elemanlar yöntemini kullanarak geoteknik mühendisliği alanındaki karmaşık problemlerin çözümünü gerçekleştiren, Hollanda menşeili bir bilgisayar yazılımıdır. Gelişimi ilk olarak, 1987’de Delft Teknoloji Üniversitesi’nde başladı. Bu yazılım geoteknik sorunları elasto-plastik davranışa uygun çözmektedir. Plaxis yazılımı sonlu eleman ağlarını üçgen elemanlar aracılığıyla modeller ve tanımlanan bölgeleri kendi içinde çözümler. Modellenen tüm bu bölgelerin her biri içerisine altı veya on beş adet düğüm ve üç veya on iki adet gerilme noktaları (Gauss noktaları) atanır, bu noktalarda zemin parametreleri analiz edilir ve toplanarak tüm model çözülmüş olur. Oluşturulan nokta ve model sayısı çözümün doğru olma olasılığını artıracaktır.
Ayrıca Plaxis yazılımı tercihe göre zeminleri veya diğer malzemeleri modellerken Lineer Elastik model, Mohr – Coulomb model, Pekleşen Zemin modeli, Pekleşmiş Zemin ile Küçük-Gerilme Rijitliği modeli, Yumuşak Zemin modeli, Yumuşak Zemin Sünme modeli, Birleşik Kaya modeli, Modifiye Cam-Kili model, NGI – ADP modeli, UDCAM – S modeli, Sekiguchi – Ohta modeli, Hoek – Brown modeli, UBC3D – PLM modeli, Beton modeli olmak üzere on dört farklı malzeme modelini kullanabilir.
Plaxis Sonlu elemanlar yöntemi
Doğada karşılaşılan durumların algılanması ve çözülmesi için matematik dili ve fizik kanunları kullanılmaktadır. Bu durumlar, sahip oldukları bazı parametreler sayesinde cebirsel, diferansiyel ve integral denklem sistemleri yardımıyla açıklanabilir. Açıklanmakta zorlanılan karmaşık sorunlarda ise çözülebilen veya anlaşılması daha kolay problemlere bölünerek daha basit bir hale getirilebilirler ve oluşturulan bu alt problemlerin çözümleri gerçekleştirilip birleştirilerek asıl problemin çözümüne ulaşılabilir.
Bu bağlamda sonlu elemanlar metodu da sonsuz sayıda serbestlik derecesi olan sistemi birbirlerine düğüm noktaları ile bağlanan sınırlı sayıda basit sonlu elemanlarla tahmin etme yöntemidir. Bu yöntemin uygulaması, gerilme problemlerinin geometrisi bilinen basit kiriş, plak, silindir, küre gibi basit şekillerle sınırlandırılıp çözülmesi ve esas problemin çözümüne ulaşılması şeklinde örneklendirilebilir. Sonlu elemanlar yöntemi kullanılarak çözülen bu problemlerin sonuçları genelde yaklaşık çözümlerdir ve doğrudan kullanılabildiği gibi bir katsayı ile düzeltilip de kullanılabilmektedir. Mühendislik alanındaki problemlerin genelde karmaşık olması nedeniyle kesin çözümler yerine yaklaşık çözümler uygun görülür.