Uzay Kafes Sistemler

Uzay kafes sistemler sanayi tesisleri, spor tesisleri, konferans salonları, tiyatro ve konser salonları, fuar alanları, benzin istasyonu kanopiler, hangarlar, sergi müze binaları gibi geniş açıklıklı istenen birçok yapıda tercih edilmektedir.

Büyük açıklı taşıyıcı sistemlerde, büyük yapı elemanlarına gereksinim duyulması sebebiyle bu yapıların ekonomik olarak tasarlanmaları oldukça güç hale gelmektedir. Özellikle yatay taşıyıcı elemanlarda (kirişlerde) oluşan eğilme momenti büyük olduğu için taşıyıcı elemanların ağırlıklarını fazla arttırmadan eğilme rijitliklerini arttırmak en uygun seçenektir. Bu durumda kirişlerin gövde kısımlarında boşluklar oluşturarak gövde yüksekliklerini attırmak ilk olarak akla gelen çözümlerden birisidir. Ancak belirli bir açıklıktan sonra gövde yüksekliği arttırılmış kirişlerin kullanımı ekonomik olmaktan uzaklaşır. Bu durumda en uygun çözüm yöntemlerinden bir tanesi gövde boşluklarını daha da arttırılarak kirişi kafes sisteme dönüştürmektedir. Bu durumda büyük açıklıklı yapılarda hem daha hafif hem de daha rijit tasarımlar oluşturmak mümkündür. Büyük açıklı yatay taşıyıcı sistem her iki doğrultuda da taşınmak istenirse kafes sistemi oluşturan çubuk elemanların üç boyutlu şekilde birbirine bağlanması en uygun çözümlerden bir tanesidir. Bu şekilde oluşturulan kafes sistemlere uzay kafes sistemler denir.

Uzay kafes sistemler yapı sistemleri içinde özel bir sınıf oluşturur. Çubuk elemanların düğüm noktalarında dönme yapmasına izin verildiği dolayısı ile çubukların sadece eksenel kuvvetler etkisinde çekme veya basınca çalıştığı varsayımı yapılır. Kafes sistemlerdeki elemanlar narindir, yanal kuvvet taşıma kapasiteleri yetersizdir bu sebeple dış kuvvetlerin sadece düğüm noktalarından uygulanması gerekir. Genellikle düğüm noktalarının serbest dönüşüne izin verilmez bu durumun kabulü bir varsayımdır. Durum böyle olsa bile kafes sistemlerdeki her bir çubuk elemanın üzerine gelen yükleri sadece eksenel kuvvet ile taşıdığı kabul edilerek hesaplanır.

Tarihte Belenger ve Brunet tarafından 1811 yılında Paris’te demir elemanlarla yapılmış yarım küre kubbe uzay kafes sistemlerin başlangıcı olarak bilinmektedir. İngiltere de ise 1815 yılında ilk demir kubbe Brighton sarayında inşa edilmiştir. Metal uzay kafes tasarımına yönelik ilk çalışmalar Alexander Graham Bell tarafından yapılmıştır. 1907 yılında uzay kafes uçak kanadı ve uçak deneylerinde kullanılmak amacıyla düğüm noktaları ve çubuklardan oluşan uzay kafes kule inşa etmiştir. 1942 yılında Dr. Max Mengeringhausen mero uzay kafes sistemi olarak bilinen ve günümüzde en çok kullanılan yöntemi bulmuştur.

Uzay kafes sistemlerin avatajları

Uzay kafes sistemler yapısal olarak birçok avantaj sağlamaktadırlar. Bunlardan bazılarını şu şekilde sıralayabiliriz: Geometrisi belirli olan her türlü yapıya uygulanabilirler. Modüller ve hafif olmaları sebebiyle büyük açıklıları geçmek kolaydır. Hafif üst yapı alt yapının da maliyetini azaltır. Hiperstatiklik dereceleri yüksek olduğu için güvenlidirler. Deprem kuşağındaki yapılarda uygulanabilecek en güvenli sistemdir. Prefabrike olarak üretilip, istenilen yerde kolaylıkla montaj yapılabilir. Süreye bağlı ortaya çıkan maliyetleri azaltır. Çelik, alüminyum gibi malzemelerden üretilip geri dönüşümü sağlanabilir veya sökülüp başka bir yere monte edilebilir. Tesisat boruları yapı içinde istenilen yönde uygulanabilir. Doğal aydınlatma sağlanabilir. İstenilen her türlü çatı kaplaması yapılabilir ve asma tavan sistemi uygulanabilir. Geniş açıklıkları kolonsuz geçme olanağı sağladığı için işlevsel olarak avantajlar sağlar. Görme alanını genişletir, ulaşım kolaylaşır, iş kazaları azalır.

Hesap ve analiz pratikleri

Uzay kafes sistemlerde analiz yapabilmek için öncelikle yapının stabil mi yoksa labil mi olduğunun belirlenmesi gerekir. Uzay kafes sistemler üç boyutlu sistemler oldukları için bir çubuk eleman her iki uçta da birbirine dik üç ötelenme olmak üzere altı serbestlik derecesine sahiptir. Her düğüm için yazılabilecek denge denklemi sayısı üçtür. Bir uzay kafes sistemin stabil olup olmadığı aşağıdaki gibi belirlenir.

m çubuk sayısı, n düğüm sayısı, r mesnet tepkisi sayısı olmak üzere; m+r=3n ise izostatik sistem m+r>3n ise hiperstatik sistem m+r<3n ise labil sistemdir.

Statik olarak kararlı bir kafes sistemde tüm çubuklar ve düğümler denge halindedir. Kafes sistemin çubuklarında oluşan kuvvetler düğüm noktaları veya çubuklara uygulanan denge denklemleri ile bulunabilir.

∑Fx=0, ∑Fy=0, ∑Fz=0, ∑Mx=0, ∑My=0, ∑Mz=0

Çubuk kuvvetleri analitik olarak iki yöntemle bulunabilir. Bunlar düğüm noktaları yöntemi ve kesim yöntemidir. Her iki yöntemde de öncelikle mesnetlerde oluşan reaksiyon kuvveti bulunur.

Düğüm noktaları yöntemine göre hesapta bütün çubuklardaki kuvvetler bulunabilir. İlk olarak iki çubuklu düğümden başlanır reaksiyon kuvveti de bilindiği için denge denklemine göre çubuk kuvvetleri bulur. Bulunan kuvvetler diğer noktaların denge denklemi için bilinen değerler olarak kullanılır ve tüm çubuklar hesaplanır. Bulunan kuvvetlerin sonucunun (+) ya da (–) çıkması durumuna göre çekme çubuğumu yoksa basınç çubuğumu olduğu belirlenir.

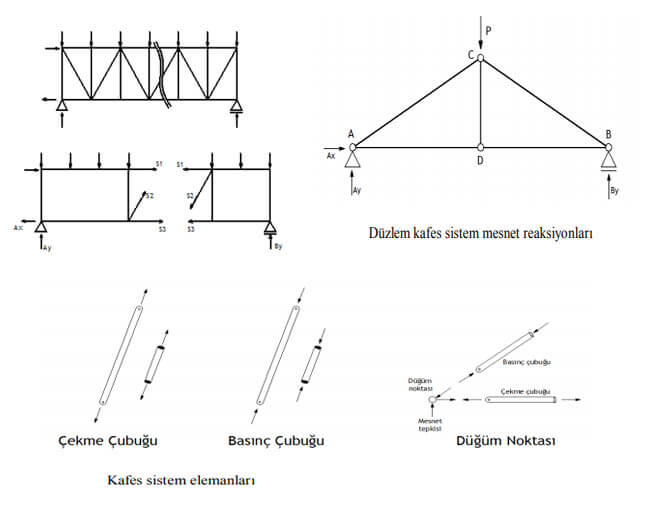
Kesme (Ritter) yöntemine göre hesap kafes sistemin belirli çubuklarındaki kuvvelerin bulunması gerektiğinde kullanılan bir yöntemdir. Düzlem kafes sistemde hesaplanması istenen çubuklardan üçü, uzay kafes sistemlerde altısı kesilerek sistem iki parçaya ayrılır. Ayrılan parçaların serbest cisim diyagramları çizilir. Mesnet reaksiyonları bulunan parçalardan herhangi birinde parçaya ait denge denklemleri yazılarak çubukların iç kuvvetleri bulunur.

Üç boyutlu kafes sistemlerin analizi doğrusal kafes sistemlere göre daha kompleks olduğundan dolayı bilgisayar programlarından yararlanılır. Analizinde kullanılan bir çok programın (SAP 2000, FRAMECAD, ANSYS) algoritması sonlu elemanlar (matris deplasman) yöntemi ile oluşturulur.